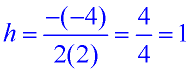How to Make an Equation Into Vertex Form
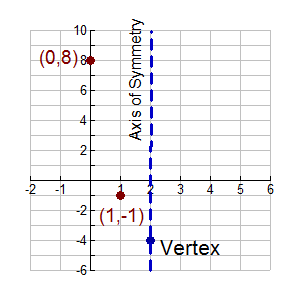
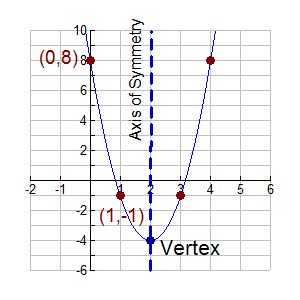
FYI: Different textbooks have different interpretations of the reference "standard form" of a quadratic function. Some say f (x) = ax 2 + bx + c is "standard form", while others say that f (x) = a(x - h)2 + k is "standard form". To avoid confusion, this site will not refer to either as "standard form", but will reference f (x) = a(x - h)2 + k as "vertex form" and will reference f(x) = ax 2 + bx + c by its full statement. When written in "vertex form": • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0). • the k represents a vertical shift (how far up, or down, the graph has shifted from y = 0). • notice that the h value is subtracted in this form, and that the k value is added.
Method 2: Using the "sneaky tidbit", seen above, to convert to vertex form:
NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation |
How to Make an Equation Into Vertex Form
Source: https://mathbitsnotebook.com/Algebra1/Quadratics/QDVertexForm.html
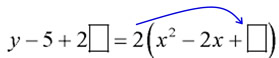
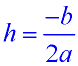 and
and